Задачи на движение

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

v=S/t, где

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с^2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.

И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8
м/с2.

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Примеров механического движения в жизни — масса. Узнайте больше у преподавателей онлайн-школы Skysmart. Каждый урок по физике — это новый эксперимент: интерактивный, живой и очень увлекательный.

Приходите на бесплатный вводный урок и начните заниматься физикой в удовольствие уже завтра!

Сколько калорий позволяет сжечь ходьба

Это интересно: жиросжигающий эффект ходьбы можно значительно усилить в разы. Для этого нужно проснуться утром чуть раньше, ничего не есть, выпить достаточно воды (ни в коем случае не пить чай или кофе с сахаром), одеться и отправляться на энергичную прогулку в течение 30 минут.

Во время такой ходьбы натощак , организм будет сжигать большое количество жира, потому что находится в состоянии голода. За 8-10 часов ночного сна наше тело успевает израсходовать практически все запасы энергетического вещества гликогена и поэтому вынуждено сжигать жир для выработки энергии

Важно помнить, что чем больше и крупнее человек, тем больше калорий он расходует в принципе. Например, человек весом в 70 кг за путь в 10 тысяч шагов будет терять 245 кал, а ходок весом в 50 кг сожжет всего 175 кал

Формула расчета сжигаемых калорий при ходьбе: количество шагов × длина шага в метрах × 0,0005 × вес человека

Для тех, кто затрудняется определить длину шага, уместно применить в расчетах среднестатистический показатель: 1 шаг = 0,7 метра. Утяжеления в виде груза на спину помогут увеличить расход калорий, то же происходит и с возрастанием интенсивности занятий. В целом при ходьбе необходимо опираться не на расчет потерянных калорий , а на изменение состава тела и увеличение выносливости. Эти показатели более адекватно передают картину оздоровления.

Средняя квадратичная скорость молекул газа — что это за параметр

Молекулы любого газа пребывают в постоянном движении. Его можно охарактеризовать с точки зрения средней их скорости или средней квадратичной скорости. Первое понятие имеет специальный термин — скорость теплового движения. Второе — средняя квадратичная скорость — величина, для которой существует специальная формула.

Для того, чтобы полностью разобраться в понятии средней квадратичной скорости молекул газа, вводится условный участник процесса — идеальный газ.

Определение

Идеальный газ — это математическая модель, потенциальную энергию которой принимают за ноль, а кинетическую характеризуют в полном объеме. Идеальный газ подходит в качестве  модели окружающих нас газов, например, обычного воздуха.

Определение

Средняя квадратичная скорость — физическая величина, отличная от средней арифметической скорости молекул, определяемая по формуле: корень квадратный из средней арифметической квадратов скоростей различных молекул.

Кинетическая энергия определяется скоростью движения молекул, поэтому зависит от температуры. Скорости молекул одного газа не одинаковы. Часть молекул движутся очень быстро, часть — с незначительной скоростью. Однако для большинства существует некое среднее значение. Если изобразить это на графике в виде параболы, такие молекулы со средней скоростью будут составлять ее верхнюю часть.

В единице объема газа содержится огромное число молекул. Поэтому, например, его давление на стенки сосуда — величина постоянная. В ином случае, если бы в единицу времени о стенку ударялось различное количество молекул, давление бы «скакало».

Из изложенного можно сделать вывод: скорость — свойство отдельной молекулы газа, а давление — характеристика их совокупности.

Средняя скорость — машина

Средняя скорость машин ЕС-1030 по Гибсону составляет 100 тыс. операций в секунду.
 

Под средней скоростью машины понимают среднюю линейную скорость одной из точек ведущего вала машины во время ее установившегося движения.
 

Для того чтобы средняя скорость машины могла оставаться постоянной, необходимо, чтобы при этой скорости имело место равновесие между работой движущих сил и работой сопротивлений. Но это равновесие может нарушаться по различным причинам.
 

Для установления козфициента нагрузки двигателя определим среднюю скорость машины v — кгк, момент трения по формуле ( 55), угловую скорость машины ( см. фиг.
 

Очевидно, что такая система позволяет на уровне программирования заботиться о том, чтобы информация была заранее считана в быстрые регистры операндов и арифметическое устройство не ожидало ее поступления из памяти. Средняя скорость машины CDC-6600 оценивается в 3 5 млн. операций в секунду, однако, как утверждают разработчики, при оптимальном программировании она может быть значительно повышена.
 

Сравнение формул ( 52) и ( 58) дает следующий вывод: коэфициент нагрузки двигателя на повороте при бортовых фрикционах в два раза меньше, чем при простом дифе-ренциале. Это снижение нагрузки достигается за счет снижения потери в тормозе, а также вследствие понижения средней скорости машины на повороте. Зависимость между коэ-фициентами нагрузки двигателя и параметром поворота показана на диаграмме фиг.
 

Регуляторы являются приборами, предназначенными для того, чтобы удерживать в возможно близких друг к другу пределах изменения средней скорости машины, вызванные изменениями движущих сил или сил сопротивлений.
 

Если бы движение машины было равномерно, если бы она шла всегда одинаково быстро, то оценка 40 км в час полностью характеризовала бы ее скорость — одну и ту же в любой момент движения. Но машина движется неравномерно; за час скорость ее много раз резко меняется, и когда нам говорят, что машина прошла в час 40 км, то это дает нам представление лишь о некоторой средней скорости машины за этот час и ничего не говорит о скорости ее в тот или другой определенный момент, в том или другом определенном месте ее пути. Час — это слишком большой промежуток времени, за который скорость движения машины может меняться много раз.
 

Средняя скорость машины при выполнении арифметики тем самым приблизительно равна 10000 операций в секунду. При выполнении логических программ быстродействие резко возрастает. В минимальном комплекте в состав процессора входит оперативная память объемом 8192 байта. Правда, объем памяти при необходимости может быть расширен до 64 Кбайт.
 

На маршруте ABCDE длиной 147 км Турист может сам выбирать способ передвижения. На обратном пути из пункта Е в пункт А он поступил по-другому: до пункта D дошел пешком, преодолев расстояние в 24 км, в пункте D пересел на лошадь и добрался до пункта В за 3 ч 20 мин, а от пункта Л до пункта А доехал на машине за 1 ч 12 мин. Определите скорость передвижения туриста на машине и на лошади, если средние скорости машины и лошади были постоянными при движении от А к S и обратно.
 

Как найти среднюю скорость движения с ускорением

Если скорость в начале движения отличается от скорости в его конце, такое движение называют ускоренным. Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.

Иными словами, если автомобиль, трогаясь с места, через секунду разогнался до скорости 10 м/сек, то его ускорение а равно 10 м в секунду за секунду а = 10 м/сек². Если в следующую секунду автомобиль остановился, то его ускорение тоже равно 10 м/сек², только уже со знаком минус: а = -10 м/сек².

Скорость движения с ускорением в конце временного отрезка вычисляется по формуле:

где V0 – начальная скорость движения, a – ускорение, t – время, за которое наблюдалось данное ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличивалась скорость или уменьшалась.

Средняя скорость за отрезок времени t вычисляется как среднее арифметическое начальной и конечной скорости:

V ср = (V0 + V) / 2.

Находим среднюю скорость: задача

Шарик толкнули по ровной плоскости с начальной скоростью V0 = 5 м/сек. Через 5 сек. шарик остановился. Чему равны ускорение и средняя скорость?

Конечная скорость шарика V = 0 м/сек. Ускорение из первой формулы равно

а = (V — V0)/ t = (0 – 5)/ 5 = — 1 м/сек².

Средняя скорость V ср = (V0 + V) / 2= 5 /2 = 2,5 м/сек.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v — понятно что такое,

S — расстояние, которое требуется найти,

t — время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

t=S/v, где v — все та же скорость,

S — расстояние, пройденный путь,

t — время, значение которого в данном случае нужно найти.

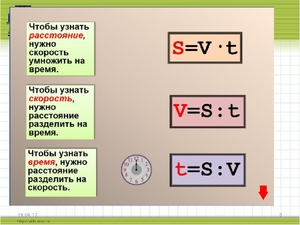
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Виды ходьбы

Скандинавская

Другое название метода — финская ходьба ( Nordic Walking ), впервые описана финскими специалистами по тренировке лыжников в летний период. Этот метод требует особой экипировки — подходящей обуви и палок, наподобие лыжных, однако более коротких и тяжелых. Ходьба с палками подразумевает дополнительную нагрузку для мышц рук и верхней части туловища и более широкую амплитудность движений. Специальная конструкция креплений в виде перчаток с обрезанными пальцами позволяет не сжимать ручку палки, а как бы опираться на нее и помогает отталкиваться от земли. Палки подбираются индивидуально и составляют около 66-68 % от роста тренирующегося. Использование палок позволяет более функционально распределить нагрузку на позвоночник и суставы конечностей, риск травмы минимален. Скорость движения может быть разной — от легкого прогулочного шага до почти бега, в среднем — 6 км/ч.

Оздоровительная

Этот способ предполагает увеличение скорости до 6-8 км/ч, почти вдвое быстрее, чем при обычной ходьбе. В таком темпе необходимо идти от 30 до 60 минут, не сбавляя шага. В целом такая скорость позволяет разговаривать, не сбивая дыхание. Эта ходьба максимально приближена к пределу физиологических возможностей человека, у нее нет специальной техники выполнения. Для людей, имеющих лишний вес, перенесших травмы и операции, очень полезной будет и обычная скорость движения, главное — идти без остановок хотя бы полчаса.

Спортивная

Олимпийский вид спорта, скорость движения при ней от 7 до 15 (17) км/ч. Его отличие от других способов хождения в том, что контакт ног с землей должен быть видимым и постоянным, а нога, вынесенная вперед, не сгибается в колене. Вторая нога ставится на землю раньше, чем оторвется первая, каждый шаг является «двухопорным». Это формирует специфическую «походку», которая забавно выглядит со стороны, но она наименее травматична из-за мягкой постановки стопы. Руки согнуты в локтях и энергично работают на уровне грудной клетки, что позволяет включить в работу практически все мышцы тела. Необходима специальная обувь, которая будет анатомически поддерживать свод стопы, иначе возможно возникновение болей. Также требуется оборудованная ровная трасса без препятствий и дефектов.

Энергетическая

Некоторые источники описывают этот метод как «индейскую походку», он направлен не на уникальные физические достижения, а на целительный психологический эффект. Метод впервые описан в книгах Карлоса Кастанеды , который вел антропологические исследования индейских племен. Суть ее заключается в том, чтобы идти друг за другом, фокусируясь на ногах впереди идущего или на земле перед собой. Идти необходимо молча, сосредоточенно, достаточно долго и монотонно. Это помогает достичь трансового состояния и «остановки внутреннего диалога», то есть бесконечного потока мыслей. Руки должны быть абсолютно свободны, возможно дополнительное утяжеление в виде рюкзака. Энергетическая ходьба дает полноценный медитативный эффект и хорошо заряжает тренирующегося.

Максимальная скорость бега человека

Следующий фактор, который влияет на скорость, – дистанция. Большинство тренированных людей могут бежать со скоростью 15-20 км/ч, но не более одного километра. Дальше их скорость начнёт падать до 12-15 км/ч. Если говорить об элитных спортсменах, то на марафонских дистанциях скорость мужчин составляет 19-21 км/ч. Женские показатели в беге на 12-15% ниже.

Учитывая дистанцию, бегуны делятся на спринтеров (100-400 м), средневиков (800-3000 м), стайеров (5000-10000 м) и марафонцев, и системы их тренировок кардинально отличаются.

Самые высокие показатели скорости характерны для спринтерских дистанций: лучшие спортсмены преодолевают 100-метровку за 10-11 секунд, а 200 м за 19-20 секунд. Такое время спортсмены показывают в основном на соревнованиях, потому что даже на тренировках их скорость на 10-20% ниже максимальной.

У стайеров и марафонцев на первом плане – выносливость, способность держать стабильную скорость на протяжении длительного времени и разогнаться к финишу. У новичков на длинных дистанциях скорость составляет 9-12 км/ч, у тренированных людей – 16-18 км/ч.

Читайте по теме: Как развить и увеличить выносливость в беге

Быстрее всех пробежал 42 км 195 м Элиуд Кипчоге в октябре 2019 года – за 1 час 59 минут и 40,2 секунды. Для этого ему пришлось бежать всю дистанцию, сохраняя скорость 21,1 км/ч. Но этот рекорд не был засчитан, поскольку условия забега были почти “лабораторными” и нарушали марафонские правила.

Действующий мировой рекорд установил он же в 2018 году на марафоне в Берлине, пробежав его за 2 часа 1 минуту и 39 секунд.

Неоднократно спринтеров и стайеров пытались сравнить, и для этого учёные вычислили дистанцию, на которой их физическая форма может быть сопоставима – это 492 метра.

Для интереса можно взглянуть, как марафонец-любитель Искандер Ядгаров и спринтер-профессионал Рушан Абдулкадеров в 2018 году выясняли, кто из них будет быстрее на дистанции 450 м.

Оздоровительная ходьба – что это?

Как упоминалось ранее, средняя скорость идущего человека составляет 4,5 км/ч. Имеет ли оздоровительный эффект для организма ходьба с этой скоростью? Да, действительно, для большинства здоровых людей будет положительный результат от таких тренировок. Но если вы определили цель – сбросить лишний вес — нужно ходить в быстром темпе. Такая скорость провоцирует активное сокращение мышц и работу суставов.

Подводя итоги, скажем, что ходьба – неимоверно полезное и вместе с тем приятное занятие, которое не требует финансовых вложений. Ходите с любой скоростью — это залог крепкого здоровья и хорошего самочувствия.

Движение по кольцевым трассам

      Задача 6. (www.reshuege.ru) Из пункта   A   круговой трассы длиной   46   км выехал велосипедист, а через   20   минут из пункта   A   следом за велосипедистом отправился мотоциклист. Через   5   минут после отправления мотоциклист догнал велосипедиста в первый раз, а еще через   46   минут после этого мотоциклист догнал велосипедиста во второй раз. Найдите скорости велосипедиста и мотоциклиста.

      Решение. К тому моменту, когда мотоциклист в первый раз догнал велосипедиста, мотоциклист ехал   5   минут, а велосипедист ехал   25   минут, причем проехали они один и тот же путь. Отсюда вытекает, что скорость мотоциклиста в   5   раз больше скорости велосипедиста.

      Таким образом, обозначив буквой   v   (км/час) скорость велосипедиста, получаем, что скорость мотоциклиста равна   5v   (км/час).

      В условии задачи дано время, прошедшее между двумя последовательными встречами мотоциклиста и велосипедиста, –   46   минут. Это время необходимо выразить в часах, чтобы все единицы измерения были согласованными:

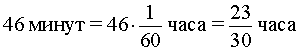
      Изобразим данные задачи, касающиеся движения мотоциклиста и велосипедиста между первой и второй встречами, на рисунке 6.

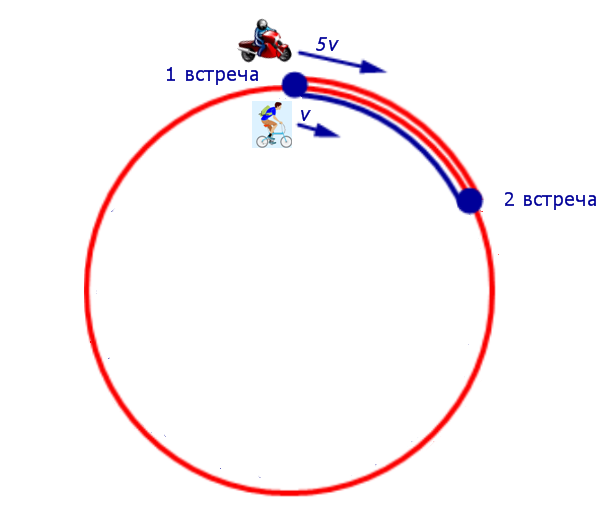
Рис. 6

      Поскольку за время часа, прошедшее от момента первой встречи до момента второй встречи, мотоциклист проехал   46   км (вся круговая трасса) плюс путь, который проехал велосипедист за часа, то можно составить следующее уравнение:

      Решая это уравнение, находим скорость велосипедиста:

v = 15 .

      Ответ. Скорость велосипедиста   15   км/час, скорость мотоциклиста   75   км/час.

      Задача 7. На дороге, представляющей собой окружность длиной   60   км, пункты   A   и   B   являются диаметрально противоположными точками. Велосипедист выехал из пункта   A   и сделал два круга. Первый круг он прошел с постоянной скоростью, после чего уменьшил скорость на   5   км/час. Время между двумя прохождениями велосипедиста через пункт   B   равно   5   часам. Найти скорость, с которой велосипедист прошел первый круг.

      Решение. Для определенности будем считать, что велосипедист двигался по кругу по часовой стрелке и рассмотрим рисунок 7.

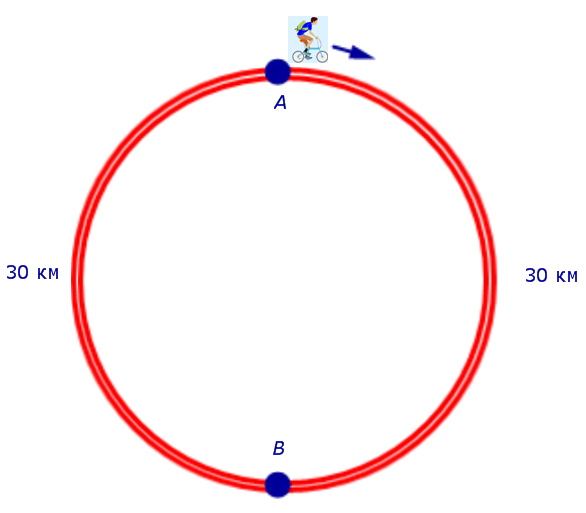
Рис. 7

      Если обозначить буквой   v   (км/час) скорость, с которой велосипедист прошел первый круг, то скорость велосипедиста на втором круге будет равна   v – 5   (км/час), и можно составить уравнение

      Решая это уравнение, находим скорость велосипедиста на первом круге:

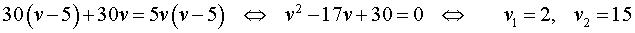
      Поскольку скорость велосипедиста на первом круге больше, чем   5   км/час, то первый корень должен быть отброшен.

      Ответ.   15   км/час.

      Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть разделы нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».

      Приемы, используемые для решения задач на выполнение работ представлены в разделе нашего справочника «Задачи на выполнение работ».

      С примерами решения задач на смеси, сплавы и растворы можно ознакомиться в разделе нашего справочника «Задачи на смеси, сплавы и растворы».

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения x(t) = x0 + v0xt + axt^2/2 x(t) — искомая координата x0 — начальная координата v0x — начальная скорость тела в данный момент времени [м/с] t — время ax — ускорение [м/с^2]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости →          → v = v0 + at → v — конечная скорость тела [м/с] v0 — начальная скорость тела [м/с] t — время → a — ускорение [м/с^2]

Задача

Найдите местоположение автобуса через 0,5 часа после начала движения, разогнавшегося до скорости 60 км/ч за 3 минуты.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

v = v0 + at
a = v — v0 / t

Так как автобус двигался с места, v0 = 0. Значит
a = v/t

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч^2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt^2/2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

x(t) = axt^2/2

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
x = 1200*0,5^2/2 = 1200*0,522= 150 км

Ответ: через полчаса координата автобуса будет равна 150 км.

Что влияет на скорость пешехода

Скорость пешехода зависит от множества факторов. Вот некоторые из них: 

• возраст — маленькие дети и люди преклонных лет ходят намного медленнее, нежели обычный трудоспособный человек
• физическая подготовка и состояние здоровья пешехода
• удобство одежды и обуви. Надеюсь, никто не станет спорить с тем, что женщина на высоких каблуках и женщина в кроссовках будут передвигаться с кардинально разной скоростью
• качество покрытия дороги, по которой идет человек;
• скорость изменяется от того, двигается человек по пересеченной местности или по тротуару
• ученые отмечают, что скорость жителей густонаселенных пунктов ниже, нежели тех, кто передвигается по безлюдной местности. 

Средняя скорость бега человека

Скорость бега зависит как от физической подготовки человека, так и от его природных данных. Первое, что влияет на скорость, – пол и возраст.

• 9-11 км/ч – средняя скорость бега ребёнка до 18 лет
• 9-12 км/ч – средняя скорость бега женщины
• 12-15 км/ч – средняя скорость бега мужчины

До пубертатного периода скорость бега мальчиков и девочек примерно одинаковая. Разрыв в цифрах начинается с момента полового созревания и обусловлен различным гормональным фоном мужчин и женщин. Поэтому к взрослому возрасту, который с точки зрения спортивных нормативов начинается с 18 лет, наблюдается ряд физиологических особенностей, объясняющих, почему женщины медленнее мужчин:

1. У женщин более слабые суставы, а значит, слабее связки и сухожилия.
2. Массовая доля жира в организме мужчины на 10-15% ниже, чем у женщины.
3. Почти на 30% у женщин предельная сила мышц конечностей ниже, чем у мужчин.
4. Объём сердца женщины меньше мужского на 10-20%.
5. Женщины дольше восстанавливаются и более подвержены стрессовым реакциям.
6. У женщин ниже гемоглобин, а значит организм хуже транспортирует кислород.
7. У мужчин уровень тестостерона в 10 раз выше женского, то есть лучше работает опорно-двигательный аппарат.
8. Каденс (шаг) женщины короче мужского.

Хотя стоит отметить, что женщины проще справляются с перепадом температур, у них лучше координация и вестибулярный аппарат. 

Не упустите

Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:

Человек проехал по тротуару на велосипеде 2 километра за 15 минут. Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.

Вот так легко запоминается формула «скорость, время, расстояние»

Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено

Для чего это нужно?

Такие расчеты полезны всем. Мы все время планируем свой день и перемещения. Имея дачу за городом, есть смысл узнать среднюю путевую скорость при поездках туда.

Это упростит планирование проведения выходных. Научившись находить эту величину, мы сможем быть более пунктуальными, перестанем опаздывать.

Вернемся к примеру, предложенному в самом начале, когда часть пути автомобиль проехал с одной скоростью, а другую — с иной. Такой вид задач очень часто используется в школьной программе. Поэтому, когда ваш ребенок попросит вас помочь ему с решением подобного вопроса, вам будет просто это сделать.

Сложив длины участков пути, вы получите общее расстояние. Поделив же их значения на указанные в исходных данных скорости, можно определить время, потраченное на каждый из участков. Сложив их, получим время, потраченное на весь путь.

Задачи на среднюю скорость (далее СК). Мы уже рассматривали задания на прямолинейное движение. Рекомендую посмотреть статьи » » и » » . Типовые задания на среднюю скорость это группа задач на движение, они включены в ЕГЭ по математике и такая задача вполне вероятно может оказаться перед вами в момент самого экзамена. Задачки простые, решаются быстро.

Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:

Если участков пути было два, тогда

Если три, то соответственно:

*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.

Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:

Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

Таким образом

Решите самостоятельно:

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

В условии сказано о трёх участках пути. СК будем искать по формуле:

Участки пути нам не даны, но мы можем без труда их вычислить:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

Вычисляем скорость:

Решите самостоятельно:

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Сказано о трёх участках пути. Формула:

Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:

Решите самостоятельно:

Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.