Изохорная теплоемкость

Теплоемкость.

Теплоемкость – свойство материала поглощать определенное количество тепла при нагревании и выделять его при охлаждении.

Удельная теплоемкость – количество тепла, необходимое для нагревания единицы количества вещества на один градус.

Формула для расчёта удельной теплоёмкости (или табл.знач.):

,

где — удельная теплоёмкость,

— количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),

— масса нагреваемого (охлаждающегося) вещества,

— разность конечной и начальной температур вещества.

В зависимости от единиц измерения количества вещества различают:

· массовую теплоемкость С , Дж / (кг К) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры;

· объемную теплоемкость С’, Дж / (м3 К) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры;

· мольную теплоемкость С_М , Дж / (кмоль К) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры.

Между различными видами теплоемкостей существует следующая зависимость:

С’ = С_М/22,4 ; С = С_М/М ; С = С’/ρ .

Различают среднюю (С_m) и истинную (С) теплоемкость:

С_m = q_1-2/(t₂–t₁) , С = lim(q/t)=dq/dt=dq/dT,

где q_1-2 – теплота, подводимая к газу в процессе нагревания от температуры t₁ до температуры t₂ .

Истинная теплоемкость – первая производная от количества теплоты, подводимой в процессе нагрева к телу, по его температуре.

Теплоемкость газа не постоянна. Она зависит от температуры и давления. Влияние давления на теплоемкость газов незначительное, поэтому обычно учитывают только влияние температуры.

Зависимости средней теплоемкости от температуры:

если тело нагревается от 0 до некоторой температуры t: С_m =a+bt/2;

если тело нагревается от температуры t₁ до температуры t₂: С_m =a+b(t₁+t₂),

где a, b, – коэффициенты, зависящие от природы газа, определяются экспериментально и приводятся в справочных таблицах.

Теплоемкость зависит от способа подвода теплоты к газу. Чаще всего используют 2 способа:

при V = const ( изохорный процесс ) — C_v;

при P = const ( изобарный процесс ) — С_р.

Теплоемкости при постоянном давлении и постоянном объеме связаны между собой следующими соотношениями:

С_р = C_v + R – уравнение Майера; С_р / C_v = к , (1)

где R — газовая постоянная, Дж /( кг К);

к — показатель адиабаты , зависит от количества атомов в молекуле газа: для одноатомных газов — к = 1,66; для двухатомных газов — к = 1,4; для трех- и многоатомных — к = 1,33 .

Анализ уравнений (1) показывает, что во время нагревания газа при P=const затрачивается тепла больше, чем при V=const.

Значение теплоемкости приближенно можно рассчитать следующим образом:

C_V= R / (к — 1) ; C_P= к R / (к – 1).

Массовую Ссм и объемную С’см теплоемость газовых смесей определяют по формулам:

C_см = Σ (C_i g_i ) ; C’_см= Σ (C’_i r_i ) ,

где C_i– массовая теплоемкость отдельного газа, Дж/(кгК);

g_i– массовые доли газов, составляющих смесь;

C’_i– объемная теплоемкость отдельного газа, Дж/(м3К);

r_i– объемные доли газов, составляющих смесь.

Количество теплоты, необходимое на нагрев тела, можно определить следующим образом:

Q = mС(t₂-t₁),

где С – удельная теплоемкость вещества.

Рассмотрим пример:

Газ (воздух) нагревается от начальной температуры t₁=25oC до t₂=130oC, масса газа m=21кг. Определить количество подведенного к воздуху тепла Q, считая удельную теплоемкость воздуха постоянной с=const=1,0301 кДж/кг·К. Выразить количество теплоты Q в килокалориях (ккал).

Решение:

Q = mС(t₂-t₁)=21·1,0301·(130-25)=2271 кДж·0,239=542,769ккал.

Ответ: Q = 2271 кДж=542,769ккал.

Первый закон термодинамики для изохорного процесса

В условиях термодинамического процесса формула элементарной работы имеет следующий вид:

\(\delta A=PdV\)

Преобразование данного выражения позволит рассчитать величину полной работы процесса:

\(A=\int_{V_{1}}^{V_{1}}{PdV}\)

В случае, когда объем сохраняет  стабильность, то есть \(dV=0\), значение интеграла будет нулевым. Исходя из этого, в изохорном процессе работа газа не наблюдается:

\(A=0\)

Изменение внутренней энергии для идеального газа рассчитывается по формуле:

\(\Delta U=\frac{i}{2}\nu R\Delta T\)

где i представляет собой количество степеней свободы, зависящее от числа атомов, которыми обладает молекула газа. В качестве примера можно рассмотреть такие вещества:

• одноатомная молекула неона обладает тремя степенями;
• пять степеней характерно для двухатомной молекулы кислорода;
• в молекуле с тремя и более атомами, как у водяного пара, насчитывается 6 степеней.

Формула внутренней энергии выходит из понятия и уравнения теплоемкости, представляет собой следующее отношение:

\(\Delta U=\nu c_{\upsilon }^{\mu }\Delta T\)

где \(c_{\upsilon }^{\mu }\) является молярной теплоемкостью в условиях постоянного объема.

Расчет количества теплоты выполняют с помощью первого начала термодинамики в условиях термодинамического процесса:

\(Q=\Delta U+A\)

Следует учитывать, что в условиях изохорного процесса газообразное вещество не выполняет работу. Исходя из этого, можно вывести формулу:

\(Q=\Delta U=\nu c_{\upsilon }^{\mu }\Delta T\)

Согласно уравнению, газ получает теплоту. Она полностью расходуется, чтобы изменять внутреннюю энергию газообразного вещества.

Теплоёмкость для различных процессов и состояний вещества код

Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).

Теплоёмкость идеального газа | код

Основная статья: Теплоёмкость идеального газа

Теплоёмкость системы невзаимодействующих частиц (например, идеального газа) определяется числом степеней свободы частиц.

Молярная теплоёмкость при постоянном объёме:

CV=dUdT=i2R,{\displaystyle C_{V}={dU \over dT}={\frac {i}{2}}R,}

где R{\displaystyle R} ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная, i{\displaystyle i} — число .

Молярная теплоёмкость при постоянном давлении связана с CV{\displaystyle C_{V}} соотношением Майера:

CP=CV+R=i+22R.{\displaystyle C_{P}=C_{V}+R={{i+2} \over 2}R.}

Теплоёмкость кристаллов | код

Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела

Существует несколько теорий теплоёмкости твердого тела:

• Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определенной точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).
• Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.
• Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.

Литература

• Артемов А. В. Физическая химия. — М.: Академия, 2013. — 288 с. — (Бакалавриат). — ISBN 978-5-7695-9550-9.
•  (недоступная ссылка)
•  (недоступная ссылка)
•  (недоступная ссылка)
• Ипполитов Е. Г., Артемов А. В., Батраков В.В. Физическая химия / Под ред. Е. Г. Ипполитова. — М.: Академия, 2005. — 448 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-1456-6.
•  (недоступная ссылка)
• Лифшиц Е. М. // Физическая энциклопедия / Ред. А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 77–78.
• Лифшиц Е. М. // Большая советская энциклопедия / Ред. А. М. Прохоров. — 3-е издание. — М.: Большая Советская Энциклопедия, 1976. — Т. 25. — С. 451.
• Сивухин Д. В. Общий курс физики. — Издание 5-е, исправленное. — М.: Физматлит, 2006. — Т. II. Термодинамика и молекулярная физика. — 544 с. — ISBN 5-9221-0601-5.
• // Большая российская энциклопедия. — М.: Большая российская энциклопедия, 2016. — Т. 32. — С. 54.

Изобарная и изохорная теплоемкость

В физике теплоемкостью называется количество теплоты, которое необходимо предоставить изучаемой системе, чтобы нагреть ее на один кельвин. Справедливо также и обратное определение, то есть теплоемкость — это количество теплоты, которое система выделяет при охлаждении на один кельвин.

Проще всего для системы определить изохорную теплоемкость. Под ней понимают теплоемкость при постоянном объеме. Поскольку система в таких условиях работу не совершает, то вся энергия расходуется на повышение внутренних энергетических запасов. Обозначим изохорную теплоемкость символом C_V, тогда можно записать:

То есть изменение внутренней энергии системы прямо пропорционально изменению ее температуры. Если сравнить это выражение, с записанным в предыдущем пункте равенством, то приходим к формуле для C_V в идеальном газе:

Данной величиной на практике неудобно пользоваться, поскольку она зависит от количества вещества в системе. Поэтому было введено понятие удельной изохорной теплоемкости, то есть величины, которую рассчитывают либо на 1 моль газа, либо на 1 кг. Обозначим первую величину символом C_Vn, вторую — символом C_Vm. Для них можно записать такие формулы:

Здесь M — молярная масса.

Изобарной называется теплоемкость при поддержании постоянного давления в системе. Примером такого процесса является расширение газа в цилиндре под поршнем при его нагревании. В отличие от изохорного, во время изобарного процесса подводимое к системе тепло расходуется на повышение внутренней энергии и на выполнение механической работы, то есть:

Энтальпия изобарного процесса представляет собой произведение изобарной теплоемкости на изменение температуры в системе, то есть:

Если рассмотреть расширение при постоянном давлении 1 моль газа, то первое начало термодинамики запишется в виде:

Последнее слагаемое получено из уравнения Клапейрона-Менделеева. Из этого равенства следует связь между изобарной и изохорной теплоемкостями:

Для идеального газа удельная молярная теплоемкость при постоянном давлении всегда больше соответствующей изохорной характеристики на величину R=8,314 Дж/(моль*К).

Краткая теория и методика выполнения работы

Удельной
теплоемкостью
вещества называется величина, равная
количеству теплоты, которую необходимо
сообщить единице массы вещества для
увеличения ее температуры на один градус
Кельвина:

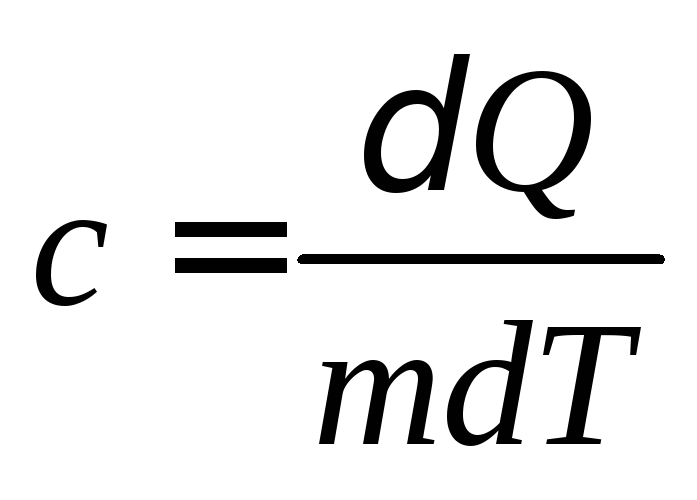. (4.1)

Теплоемкость
одного моля вещества называется молярной
теплоемкостью:

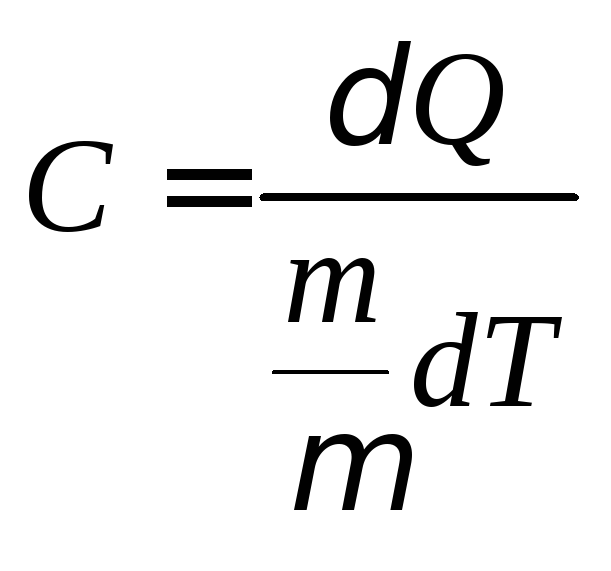, (4.2)

где
m – масса, µ – молярная масса вещества,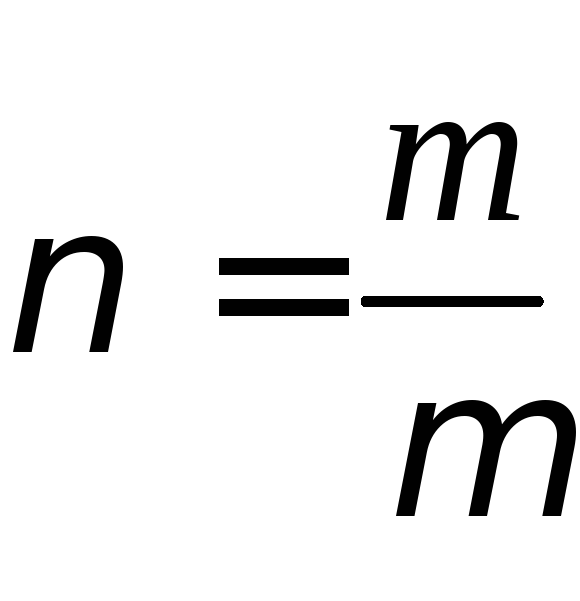– число молей газа.

Значение
теплоемкости газов зависит от условий
их нагревания. В соответствии с первым
законом термодинамики количество
теплоты,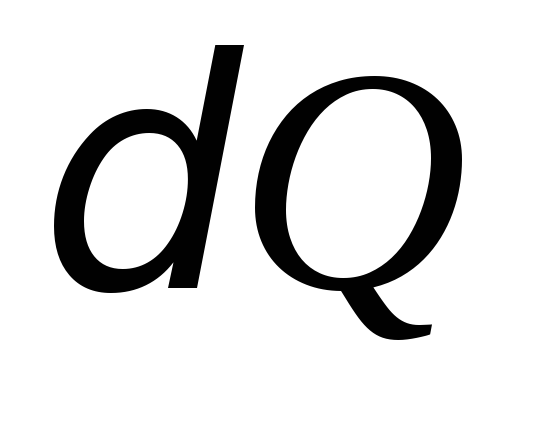
сообщенное системе, расходуется на
увеличение ее внутренней энергиии на совершение системой работыпротив внешних сил:

. (4.3)

Изменение
внутренней энергии идеального газа в
случае изменения его температурыравно:

, (4.4)

здесь
– число степеней свободы молекулы газа,
под которым подразумевается число
независимых координат, полностью
определяющих положение молекулы в
пространстве;– универсальная газовая постоянная.

При
расширении газа система совершает
работу:

. (4.5)

Если
газ нагревать при постоянном объеме
(),
тои, согласно (4.3), все полученное газом
количество теплоты расходуется только
на увеличение его внутренней энергии.
Следовательно, учитывая (4.4), молярная
теплоемкость идеального газа при
постоянном объеме будет равна:

. (4.6)

Если
газ нагревать при постоянном давление
(),
то полученное газом количество теплоты
расходуется на увеличение его внутренней
энергиии совершение газом работы: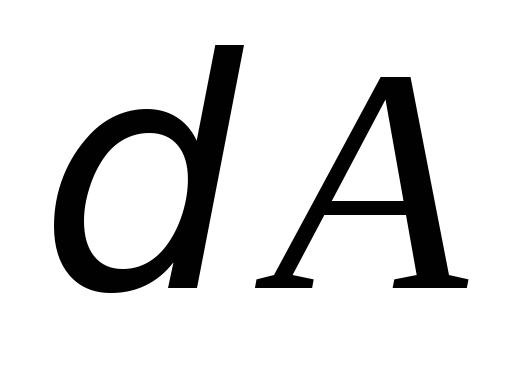

.

Тогда
молярная теплоемкость идеального газа
при постоянном давлении определяется
следующим образом:

. (4.7)

Используя
уравнение состояния идеального газа
(уравнение Клапейрона–Менделеева),
можно показать, что для одного моля газа
справедливо соотношение:

,

поэтому:

.

Последнее выражение
называют уравнением Майера. Из него,
учитывая (4.6), получаем:

. (4.8)

Отношение
теплоемкостейобозначаюти называют показателем адиабаты или
коэффициентом Пуассона:

. (4.9)

Адиабатным
называется процесс, протекающий в
термоизолированной системе, т.е. без
теплообмена с окружающей средой,.

На
практике он может быть осуществлен в
системе, окруженной теплоизоляционной
оболочкой, но поскольку для теплообмена
необходимо некоторое время, то адиабатным
можно считать также процесс, который
протекает так быстро, что система не
успевает вступить в теплообмен с
окружающей средой.

Первый
закон термодинамики для адиабатного
процесса имеет вид.
Знак минус говорит о том, что при
адиабатном процессе система может
совершать работу только за счет внутренней
энергии. С учетом (4.4)–(4.6) имеем:

. (4.10)

Продифференцировав
уравнение Клапейрона–Менделеева,
получим:

.

Выразим
из негои подставим в формулу (4.10):

.

Выразив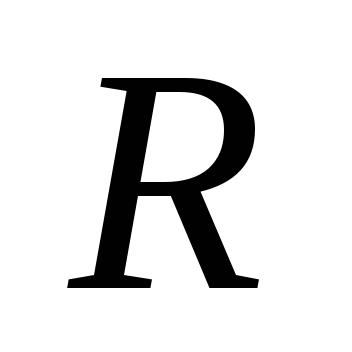из уравнения Майера и учитывая соотношение
(4.8), получим:

.

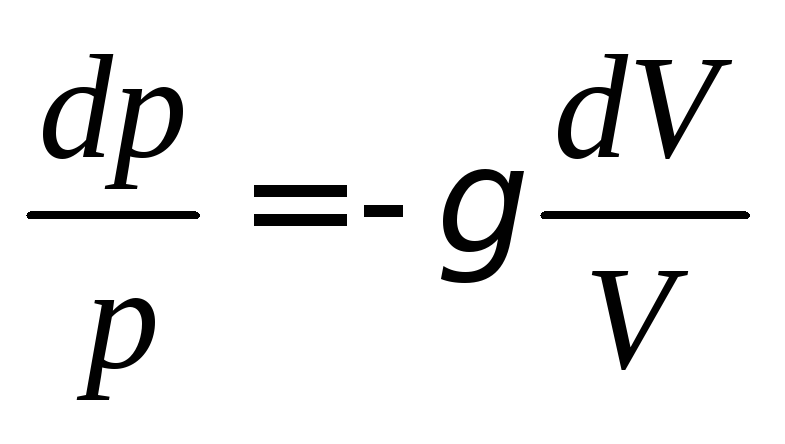Интегрируя
данное дифференциальное уравнение при
условииполучим выражение:

.
(4.11)

Уравнение
(4.11) называется уравнением адиабаты или
уравнением Пуассона.

Метод
определения показателя адиабаты,
предложенный Клеманом и Дезормом (1819
г.), основывается на изучении параметров
некоторой массы газа, переходящей из
одного состояния в другое двумя
последовательными процессами –
адиабатным и изохорным. Эти процессы
на диаграмме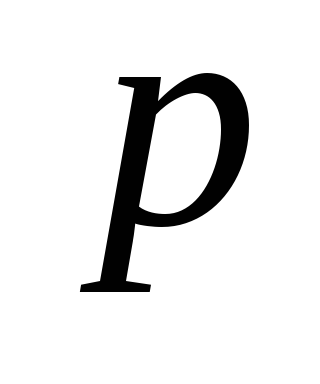–(рис. 4.1) изображены кривыми соответственно
1–2 и 2–3.

Если
в сосуд, соединенный с дифференциальным
датчиком давления, накачать воздух и
подождать до установления теплового
равновесия с окружающей средой, то в
этом начальном состоянии 1 газ имеет
параметры,,,
причем температура газа в сосуде равна
температуре окружающей среды,
а давлениенемного больше атмосферного.

Если
теперь на короткое время соединить
сосуд с атмосферой, то произойдет
адиабатное расширение воздуха. При этом
воздух в сосуде перейдет в состояние
2, его давление понизится до атмосферного.
Масса воздуха, оставшегося в сосуде,
которая в состоянии 1 занимала часть
объема сосуда, расширяясь, займет весь
объем.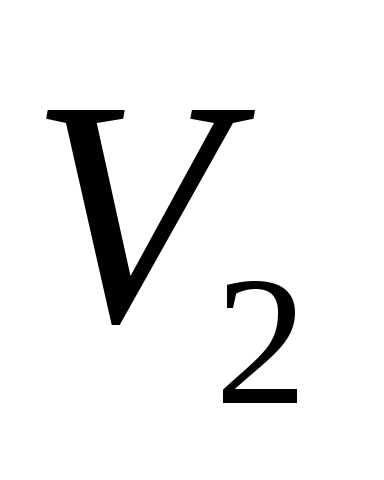
При этом температура воздуха, оставшегося
в сосуде, понизится до.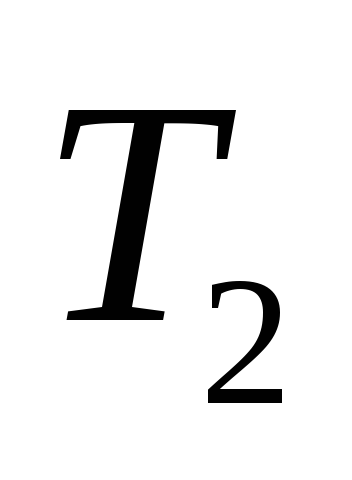
Поскольку процесс 1–2 – адиабатный, к
нему можно применить уравнение Пуассона
(4.11):

или.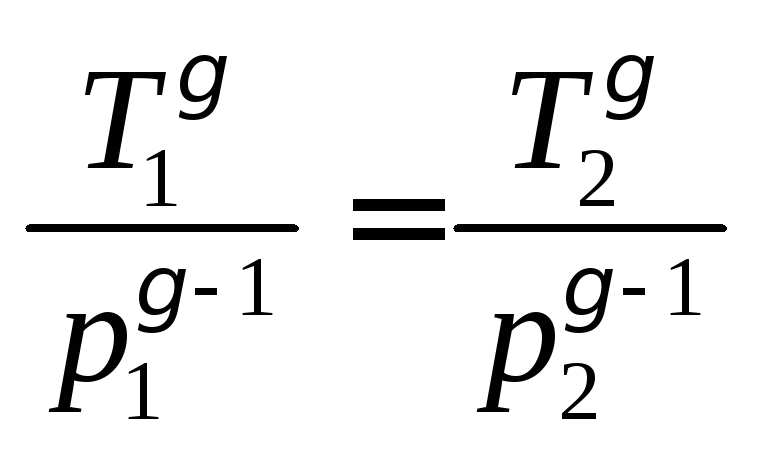

Отсюда:

. (4.12)

После
кратковременного соединения сосуда с
атмосферой охлажденный из-за адиабатного
расширения воздух в сосуде будет
нагреваться (процесс 2–3) до температуры
окружающей средыпри постоянном объеме.
При этом давление в сосуде поднимется
до.

Поскольку
процесс 2–3 – изохорный, к нему можно
применить закон Шарля:

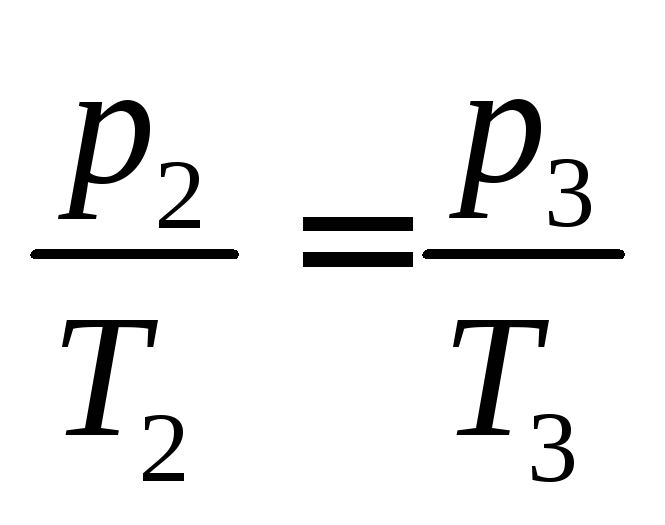или

. (4.13)

Из уравнений (4.12)
и (4.13) получим:

.

Прологарифмируем
это выражение:

.

Поскольку
избыточные давленияи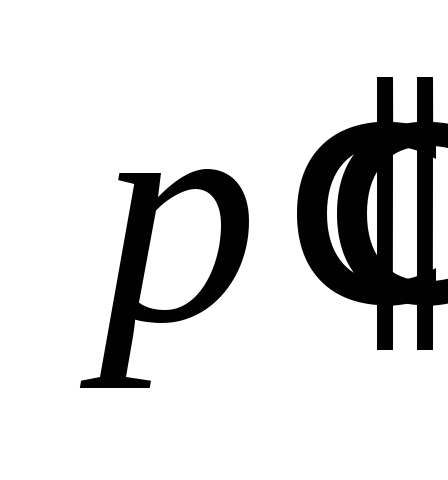очень малы по сравнению с атмосферным
давлением,
а также учитывая, что при,
будем иметь:

.

Откуда:

. (4.14)

Избыточные
давленияи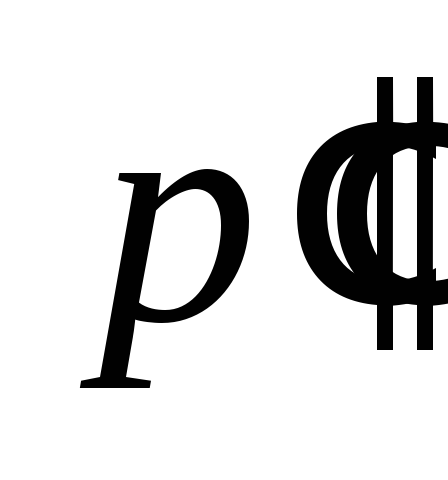измеряют с помощью дифференциального
датчика давления.

Идеальный газ

Идеальным называется такой газ, частицы которого считаются материальными точками, то есть не имеют размеров, но обладают массой, и у которого вся внутренняя энергия состоит исключительно из кинетической энергии движения молекул и атомов.

Любой реальный газ в идеале никогда не будет удовлетворять описанной модели, поскольку его частицы все же имеют некоторые линейные размеры и взаимодействуют между собой с помощью слабых ван-дер-ваальсовых связей или химических связей другого типа. Однако при низких давлениях и высоких температурах расстояния между молекулами велики, а их кинетическая энергия превышает потенциальную в десятки раз. Все это позволяет применять с высокой степенью точности идеальную модель для реальных газов.

Вопросы по теме «Теплоемкость идеального газа»

Вопрос 1. Что такое теплоемкость идеального газа?

Ответ. Когда газу сообщается определенное количество теплоты, меняется его температура.

Вопрос 2. Что такое молярная и удельная теплоемкость идеального газа?

Ответ. Молярная и удельная теплоемкости активно используются в термодинамике. Молярная теплоемкость – это теплоемкость одного моля вещества. 

Удельная теплоемкость – теплоемкость единичной массы вещества.

Вопрос 3. Как определяется теплоемкость газа при изопроцессах?

Ответ. 

При изотермическом процессе T=const. Теплоемкость равна плюс/минус бесконечности.
При адиабатном процессе нет теплообмена с окружающей средой, теплоемкость равна нулю.
При изохорном процессе газ не совершает работы, а теплоемкость равна:

Здесь i – количество степеней свободы молекул газа. Для одноатомных газов i=3, для двухатомных i=5.

При изобарном процессе теплоемкость определяется соотношением Мейера:

Вопрос 4. Как еще связаны теплоемкости при постоянном давлении и постоянном объеме?

Ответ. Отношение теплоемкостей при постоянном давлении и постоянном объеме обозначается греческой буквой «гамма» и называется показателем адиабаты. 

Вопрос 5. Как называются процессы, в которых теплоемкость газа остается неизменной?

Ответ. Такие процессы называются политропными. Адиабатный процесс – частный случай политропного процесса.

Теплоемкость реального газа не равна теплоемкости идеального газа и может сильно отличаться.

Нужна помощь в решении задач и выполнении других заданий? Специальный студенческий сервис готов оказать ее!

Задачи по теме «Теплоемкость идеального газа» с решениями

Повторение и практика – залог успеха в любом деле. И решение задач не исключение. Поэтому не забываем держать под рукой памятку по задачам и полезные формулы

Задача №1. Определить удельную теплоемкость идеального газа

Условие

Определить молярную массу M двухатомного газа и его удельные теплоемкости, если известно, что разность cр — cv удельных теплоемкостей этого газа равна 260 Дж/(кг*К)

Решение

По определению:

Значит, газ из задачи – кислород. Если кто не понял, как это определяется, учитесь пользоваться таблицей Менделеева.

Считаем удельные теплоемкости:

Ответ: 32 г/моль; 649 Дж/кг*К; 909 Дж/кг*К.

Задача №2. Удельная теплоемкость

Условие

Плотность некоторого газа при нормальных условиях ρ = 1,25 кг/м3. Отношение удельных теплоемкостей γ = 1,4. Определить удельные теплоемкости cv и сp этого газа.

Решение

Исходя из отношения удельных теплоемкостей, можно сделать вывод, что газ – двухатомный, i=5. При постоянном объеме удельная теплоемкость равна:

Молярную массу можно найти из уравнения Клапейрона-Менделеева:

Отсюда:

Ответ: 742 Дж/кг*К; 1039 Дж/кг*К.

Задача №3. Молярная теплоемкость

Условие

Вычислить молярные теплоемкости газа, зная, что его молярная масса М = 4∙10 3 кг/моль и отношение удельных теплоемкостей ср/сv = 1,67.

Решение

Удельные теплоемкости равны:

Можно найти:

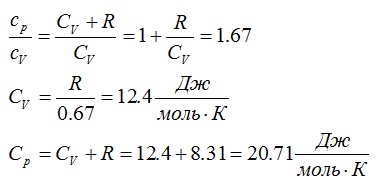
Ответ: 12,4 Дж/моль*К; 20,71 Дж/моль*К

Задача №4. Теплоемкость при изопроцессах

Условие

На рисунке изображен изотермический процесс с газом постоянной массы. Сравните теплоемкость в процессе АВ с теплоемкостью этой же массы газа в изохорном процессе.

Решение

Теплоемкость при изохорном процессе является постоянной величиной. При изотермическом процесса она равна бесконечности. Значит, теплоемкость в процессе АВ больше.

Ответ: Теплоемкость в процессе АВ больше.

Задача №5. Теплоемкость при политропическом процессе

Условие

Найдите молярную теплоемкость идеального газа при политропическом процессе pVn = const, если показатель адиабаты газа равен γ. При каких значениях показателя политропы n теплоемкость газа будет отрицательной?

Решение

Запишем первое начало термодинамики, выражения для работы и изменения внутренней энергии в политропическом процессе соответственно:

Если количество вещества и изменение температуры принять равными единице, это выражение будет равно молярной теплоемкости (по определению теплоемкости):

Ответ: см. выражение выше.

Таблица удельной теплоемкости пищевых продуктов

В таблице приведены значения средней удельной теплоемкости пищевых продуктов (овощей, фруктов, мяса, рыбы, хлеба, вина и т. д.) в диапазоне температуры 5…20°С и нормальном атмосферном давлении.

Таблица удельной теплоемкости продуктов питания

Продукты	C, Дж/(кг·К)
Абрикосы	3770
Ананасы	3684
Апельсины	3730
Арбуз	3940
Баклажаны	3935
Брюква	3810
Ветчина	2140
Вино крепленое	3690
Вино сухое	3750
Виноград	3550
Вишня	3650
Говядина и баранина жирная	2930
Говядина и баранина маложирная	3520
Горох	3684
Грибы свежие	3894
Груши	3680
Дрожжи прессованные	1550…3516
Дыни	3850
Ежевика	3642
Земляника	3684
Зерно пшеничное	1465…1549
Кабачки	3900
Капуста	3940
Картофель	3430
Клубника	3810
Колбасы	1930…2810
Крыжовник	3890
Лимоны	3726
Лук	2638
Макароны не приготовленные	1662
Малина	3480
Мандарины	3770
Маргарин сливочный	2140…3182
Масло анисовое	1846
Масло мятное	2080
Масло сливочное	2890…3100
Масло сливочное топленое	2180
Мед	2300…2428
Молоко сухое	1715…2090
Морковь	3140
Мороженое (при -10С)	2175
Мука	1720
Огурцы	4060
Пастила	2090
Патока	2512…2700
Перец сладкий	3935
Печенье	2170
Помидоры	3980
Пряники	1800…1930
Редис	3970
Рыба жирная	2930
Рыба нежирная	3520
Салат зеленый	4061
Сало топленое	2510
Сахар кусковой	1340
Сахарный песок	720
Свекла	3340
Свинина жирная	260
Свинина нежирная	3010
Слива	3750
Сметана	3010
Смородина черная	3740
Сода	2256
Соль поваренная (2% влажности)	920
Спаржа	3935
Сыр жирный	2430
Творог	3180
Телятина жирная	3180
Телятина нежирная	3520
Тесто заварное	2910
Тыква	3977
Хлеб (корка)	1680
Хлеб (мякиш)	2800
Черешня	3770
Чернослив	3181
Чеснок	3140
Шоколад	2340…2970
Шпинат	3977
Яблоки	3760
Яйцо куриное	3180

Кроме таблиц удельной теплоемкости, вы также можете ознакомиться с подробнейшей таблицей плотности веществ и материалов, которая содержит данные по величине плотности более 500 веществ (металлов, пластика, резины, продуктов, стекла и др.).

1. Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача. Учебник для вузов, изд. 3-е, перераб. и доп. — М.: «Энергия», 1975.
2. Тепловые свойства металлов и сплавов. Справочник. Лариков Л. Н., Юрченко Ю. Ф. — Киев: Наукова думка, 1985. — 439 с.
3. Физические величины. Справочник. А. П. Бабичев, Н. А. Бабушкина, А. М. Братковский и др. Под ред. И. С. Григорьева — М.: Энергоатомиздат, 1991. — 1232 с.
4. Еремкин А. И., Королева Т. И. Тепловой режим зданий: Учебное пособие. — М.: Издательство ACB, 2000 — 368 с.
5. Кириллов П. Л., Богословская Г. П. Тепломассобмен в ядерных энергетических установках: Учебник для вузов.
6. Михеев М. А., Михеева И. М. Основы теплопередачи. Изд. 2-е, стереотип. М.: «Энергия», 1977. — 344 с. с ил.
7. Казанцев Е. И. Промышленные печи. Справочное руководство для расчетов и проектирования.
8. Франчук А. У. Таблицы теплотехнических показателей строительных материалов, М.: НИИ строительной физики, 1969 — 142 с.
9. Добрынин В. М., Вендельштейн Б. Ю., Кожевников Д. А. Петрофизика: Учеб. для вузов. 2-ое изд. перераб. и доп. под редакцией доктора физико-математических наук Д. А. Кожевникова — М.: ФГУП Издательство «Нефть и газ» РГУ нефти и газа им. И.М. Губкина, 2004. — 368 с., ил.
10. В. Блази. Справочник проектировщика. Строительная физика. М.: Техносфера, 2005. — 536 с.
11. Енохович А. С. Справочник по физике. М.: «Просвещение», 1978. — 415 с. с ил.
12. Строительная теплотехника СНиП II-3-79. Минстрой России — Москва 1995.
13. Мустафаев Р. А. Теплофизические свойства углеводородов при высоких параметрах состояния. М.: Энергоатомиздат, 1991. — 312 с.
14. Новиченок Н. Л., Шульман З. П. Теплофизические свойства полимеров. Минск, «Наука и техника» 1971. — 120 с.
15. Шелудяк Ю. Е., Кашпоров Л. Я. и др. Теплофизические свойства компонентов горючих систем. М., 1992. — 184 с.

Воздух — идеальный газ

Прежде чем раскрывать вопрос теплоемкости воздуха, рассмотрим модель идеального газа. В соответствии с ней полагают, что система состоит из невзаимодействующих друг с другом частиц, которые хаотично движутся в ограниченном объеме пространства. Скорости частиц подчиняются классическому распределению Максвелла-Больцмана. Модель также предполагает, что частицы являются безразмерными.

Насколько точно в приведенную модель вписывается воздушная смесь? Известно, что воздух состоит в основном из молекул азота и кислорода. Эти молекулы являются химически нейтральными. Существующие между ними ван-дер-ваальсовые взаимодействия являются очень слабыми, поэтому их при выполнении термодинамических расчетов можно не учитывать. Что касается размеров молекул, то ими также можно пренебречь, так как расстояния между ними на несколько порядков больше. Таким образом, воздух очень хорошо описывается моделью идеального газа.

Формулы изохорной и изобарной теплоемкостей воздуха

Сначала рассмотрим изохорную величину. Обозначим ее CV. Первое начало термодинамики, которое следует из закона сохранения энергии, для изохорного процесса выглядит следующим образом:

То есть все тепло H, подводимое к системе, идет на увеличение ее внутренней энергии. Изменение величины U можно записать так:

С другой стороны, если воспользоваться универсальным уравнением состояния идеальной газовой системы, то формула для dU запишется в виде:

Здесь z — количество степеней свободы молекул, n — количество вещества, R — постоянная, dT — изменение температуры. Выражение выше следует из того факта, что внутренняя энергия идеального газа в точности равна кинетической энергии его молекул.

Из сравнения двух равенств получаем формулу для изохорной теплоемкости:

В случае воздуха z=5, поскольку он на 99 % состоит из двухатомных молекул азота и кислорода (двухатомные молекулы имеют 3 поступательные и 2 вращательные степени свободы). Полагая n=1 моль, приходим к формуле изохорной молярной теплоемкости воздуха:

Напомним, что постоянная R равна 8,314, тогда CV = 20,785 Дж/(моль*К).

Теперь определим молярную изобарную теплоемкость воздуха. Поскольку в результате изобарного нагрева газ расширяется, то он выполняет некоторую работу. Первое начало термодинамики в этом случае принимает вид:

Энтальпия H через изобарную теплоемкость CP для 1 моль вещества запишется так:

Работу газа с использованием уравнения Клапейрона-Менделеева можно записать так:

Эти выражения позволяют записать следующее соотношение изобарной и изохорной теплоемкостей:

Подставляя величину CV для воздуха, получаем изобарную молярную теплоемкость для него:

Таким образом, величина CP оказывается больше, чем CV.

Какой процесс называется изохорным, условия протекания

Определение

Изохорным процессом называют термодинамический процесс, протекающий при условии постоянного объема.

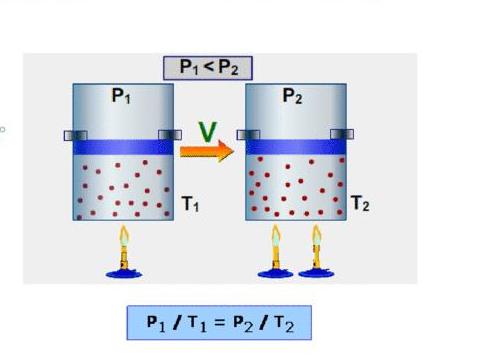
Изохорный процесс можно наблюдать опытным путем. Для этого необходимо повышать или понижать температуру вещества в газообразном или жидком состоянии, находящегося в сосуде и сохраняющего стабильность объема. В случае, когда манипуляции производят с идеальным газом, его давление и температура будут изменяться прямо пропорционально, согласно закону Шарля. Для реальных газов данная закономерность не применима.

История возникновения теории, кто открыл, формула

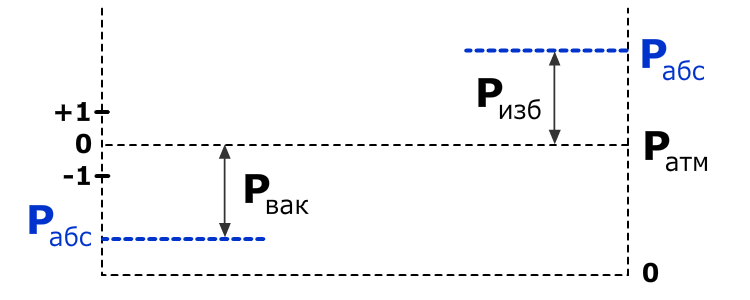
Изучение изохорного процесса связывают с Гийомом Амонтоном. Работа ученого под названием «Парижские мемуары», написанная в 1702 году, посвящена исследованию характеристик газообразного вещества, помещенного в фиксированный объем, который составляет часть «воздушного термометра». Равновесие жидкости в данных условиях объясняется воздействием на нее давления газа, находящегося в сосуде, и атмосферного давления. Если температура среды повышается, показатели давления в резервуаре возрастают. При этом определенный объем жидкости вытесняется в выступающую трубку. Зависимость между такими характеристиками процесса, как температура и давление, представлена на рисунке.

В 1801 году были опубликованы два эссе исследователя Джона Дальтона с описанием эксперимента, результаты которого демонстрируют одинаковое расширение всех газов и паров при постоянном давлении и изменении температуры, когда начальная и конечная температура одинакова. В итоге был сформулирован закон Гей-Люссака. Ученый, в честь которого явление получило название, экспериментальным путем подтвердил одинаковое расширение различных газообразных веществ и вывел коэффициент, практически равный коэффициенту, полученному Дальтоном. Благодаря объединению данной закономерности с законом Бойля-Мариотта, был описан изохорный процесс.

Ежедневные примеры

Легко представить себе изохорный процесс, нужно только думать о процессе, который происходит в постоянном объеме; то есть, в котором контейнер, содержащий вещество или материальную систему, не изменяется в объеме.

Примером может служить случай (идеального) газа, заключенного в закрытый контейнер, объем которого не может быть изменен никакими средствами, к которым подводится тепло. Предположим, в случае газа, заключенного в бутылку.

Передача тепла газу, как уже объяснялось, в конечном итоге приведет к увеличению или увеличению его внутренней энергии..

Обратный процесс будет происходить с газом, заключенным в контейнер, объем которого не может быть изменен. Если газ охлаждается и отдает тепло окружающей среде, тогда давление газа будет уменьшаться, а значение внутренней энергии газа будет уменьшаться..

Идеальный цикл Отто

Цикл Отто является идеальным случаем цикла, используемого бензиновыми двигателями. Тем не менее, его первоначальное использование было в машинах, которые использовали природный газ или другое топливо в газообразном состоянии.

В любом случае идеальный цикл Отто является интересным примером изохорного процесса. Это происходит, когда сгорание смеси бензина и воздуха происходит мгновенно в двигателе внутреннего сгорания..

В этом случае происходит повышение температуры и давления газа внутри цилиндра, при этом объем остается постоянным.